publications

2025

1. 

   Gravity-driven thin films: flow and dissolution

   Simeon Djambov

   Ph.D. thesis, EPFL , 2025

   Abs DOI

   The present thesis deals with gravity-driven thin-film flows in various configurations. We study the late-time drainage of a fixed liquid volume on a saddle topography, where the concurrent convergent and divergent natures of the flow render the pure-drainage equation, accounting only for the driving tangential component of gravity, singular. In fact, a hydrostatic boundary layer regularises the flow in the vicinity of the saddle point. We characterise it and discuss its universality to all topographies, presenting saddle points.
   We investigate the linear instability of uniform film flows at an imposed flow rate over inclined soluble surfaces, believed to carve an array of rills in the direction of the flow, known as linear karren patterns. We obtain a closed-form local dispersion relation and numerically calculate a global one.
   In the realm of spatially distributed volumetric sources, we obtain an analytical solution to the free-surface Stokes equations on spheres and cylinders in the case of uniform vertical volumetric flux through the interface, modelling rainfall. We analyse the linear stability of film flows on an inclined plane sustained by rain or vapour condensation. We apply a weakly non-parallel asymptotic method that is in perfect agreement with global calculations, and predict the linearly most amplified frequency.
   We explore the parallels between all of these configurations: late-time drainage of a fixed liquid volume, film flow with an imposed flow rate, as well as different spatially distributed sources, such as rain or vapour condensation. We believe that the unified framework behind all of them holds untapped potential for applications in geomorphogenesis involving thin-film flows. Finally, we construct an advection-less model for erosion by dilution-driven dissolution and apply it to the evolution of symmetric soluble blocks under rainfall.

2024

1. 

   Stability of a liquid layer draining around a horizontal cylinder: Interplay of capillary and gravity forces

   Shahab Eghbali, Simeon Djambov, and François Gallaire

   Physical Review Fluids, 2024

   Abs DOI PDF Bib

   We study the drainage of a viscous liquid film coating the outside of a solid horizontal cylinder, where gravity acts vertically. We focus on the limit of large Ohnesorge numbers \(𝑂h\), where inertia is negligible compared to viscous effects. We first study the evolution of the axially invariant draining flow, initiated at rest with uniform film thickness \( δ\). Non-linear simulations indicate that for each \( δ\), there is a threshold in the Bond number (\(Bo\)), which compares the gravitational effects with surface tension, above which the draining liquid bulk ruptures. This critical \(Bo \)  is found to scale inversely with \( δ\), defines the existence of a quasi-stationary pendant liquid curtain remaining sustained below the cylinder by surface tension. The interface of the pendant curtain is unconditionally linearly unstable and is prone to Rayleigh-Plateau-like, capillarity-driven, and Rayleigh-Taylor, gravity-driven, instabilities. The linear stability of the quasi-static state along with an energy analysis of the unstable mode illustrates that while the Rayleigh-Taylor instability is always present, capillary effects dominate the instability at small \(Bo\), which promotes the formation of pearls enveloping the cylinder. In contrast, at large \(Bo\), capillarity acts in a stabilising way and the instability is purely gravity-driven, forming underside modulations. We present the asymptotic energy repartition representing the different physical mechanisms at play in the instability of the saturated curtains for a wide range of \( \{Bo, δ\}\). The results of the linear analysis agree with the pre-existing experiments of de Bruyn [Phys. Fluids 9(6), 1599 (1997)] and non-linear simulations of Weidner et al. [J. Colloid Interface Sci. 187, 243 (1997)] in the limit of a thin film and extend the results for thick films. Additionally, based on the volume made available for droplet growth by the development of the most linearly amplified wavelength, we build a tentative regime diagram that predicts the final patterns emerging from the pendant curtain, namely an array of saturated pearls or pendant drops or the onset of three-dimensional droplet pinch-off. Furthermore, a transient growth analysis accounting for the time-evolution of the base state towards a saturated curtain conclusively demonstrates that the initial flow evolution does not result in altering the most amplified wavelength, thus rationalizing a posteriori the asymptotic analysis to predict the fate of the three-dimensional patterns.

   @article{eghbali2024stability,
     title = {Stability of a liquid layer draining around a horizontal cylinder: Interplay of capillary and gravity forces},
     author = {Eghbali, Shahab and Djambov, Simeon and Gallaire, Fran{\c{c}}ois},
     journal = {Physical Review Fluids},
     volume = {9},
     pages = {063903},
     year = {2024},
     doi = {10.1103/PhysRevFluids.9.063903},
   }

2023

1. 

   Boundary-layer approach to the linear karren instability

   Simeon Djambov, and François Gallaire

   Journal of Fluid Mechanics, 2023

   Abs DOI PDF Bib

   The present paper concerns the linear fate of transverse perturbations in a gravity-driven, thin-film flow over a soluble substrate. We propose a reduced-order model, based on a boundary-layer treatment of the solute transport and a depth-integration of the Stokes equations, using two extended lubrication methodologies found in the literature. We obtain a closed-form dispersion relation, which we compare to a previous, fully resolved analytical investigation (Bertagni and Camporeale, J. Fluid Mech., vol. 913, 2021, A34). The results allow us to distil the essential physical mechanisms behind the instability.

   @article{djambov2023boundary,
     title = {Boundary-layer approach to the linear karren instability},
     author = {Djambov, Simeon and Gallaire, Fran{\c{c}}ois},
     journal = {Journal of Fluid Mechanics},
     volume = {977},
     pages = {R3},
     year = {2023},
     publisher = {Cambridge University Press},
     doi = {10.1017/jfm.2023.932},
   }

2021

1. 

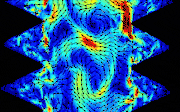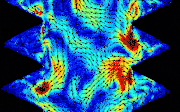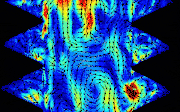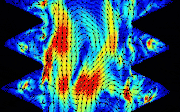   Asymptotic turbulent friction in 2D rough-walled flows

   Alexandre Vilquin, Julie Jagielka, Simeon Djambov, and 6 more authors

   Science Advances, 2021

   Abs DOI PDF Bib

   In turbulent rough-walled flows, the 2D friction–roughness relation differs from its 3D counterpart. The friction \(f \)  is the property of wall-bounded flows that sets the pumping cost of a pipeline, the draining capacity of a river, and other variables of practical relevance. For highly turbulent rough-walled pipe flows, \(f \)  depends solely on the roughness length scale \(r\), and the \(f \)–\(r \)  relation may be expressed by the Strickler empirical scaling \(f ∝r^{1/3}\). Here, we show experimentally that for soap film flows that are the two-dimensional (2D) equivalent of highly turbulent rough-walled pipe flows, \(f ∝r \)  and the \(f \)–\(r \)  relation is not the same in 2D as in 3D. Our findings are beyond the purview of the standard theory of friction but consistent with a competing theory in which \(f \)  is linked to the turbulent spectrum via the spectral exponent \( α\): In 3D, \( α= 5/3\), and the theory yields \(f ∝r^{1/3}\); in 2D, \(α= 3\), and the theory yields \(f ∝r\).

   @article{vilquin2021asymptotic,
     title = {Asymptotic turbulent friction in 2D rough-walled flows},
     author = {Vilquin, Alexandre and Jagielka, Julie and Djambov, Simeon and Herouard, Hugo and Fischer, Patrick and Bruneau, Charles-Henri and Chakraborty, Pinaki and Gioia, Gustavo and Kellay, Hamid},
     journal = {Science Advances},
     volume = {7},
     number = {5},
     pages = {eabc6234},
     year = {2021},
     publisher = {American Association for the Advancement of Science},
     doi = {10.1126/sciadv.abc6234},
   }